Forth Code for Electrocrabs in 1984 ChipWits Deciphered

The ChipWits team has been in major Nostalgia mode for the past month or two while we extract data from some old 5.25″ and 3.5″ disks containing the original Forth code for ChipWits. Thanks again to our many fans, including this one who had his own copy of the source code, our efforts are beginning to bear fruit!

In this devlog post, we’re going to learn a little bit about Electrocrabs and take a peek at the original MacForth source code for the game ChipWits from 1984. Come along for the ride!

What are Electrocrabs?

Electrocrabs are one of a few “baddies” that inhabit the levels of the original game. They add a bit of fun randomness to the game as they step in front of your robot at just the wrong time, causing damage. Left to their own devices, electrocrabs creep towards the ChipWit and begin to suck its fuel.

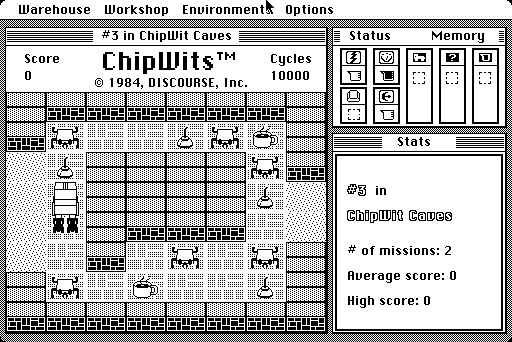
Reverse Engineered Algorithm

One of the things I was most eager to see in the original source is the precise algorithm (procedure) for how Electrocrabs move. While rebooting the game, I resorted to a frame-by-frame analysis of video of the gameplay in an emulator in order to reverse-engineer the algorithm. My conclusion was that the algorithm works approximately as follows:

1. Each second, the Electrocrab has a 25% chance of turning
2. Each second, the Electrocrab has a 12.5% chance of “pouncing”
3. Each second, the Electrocrab has a 37.5% chance of moving toward the current location of the ChipWit
4. If the Electrocrab is one square away from the ChipWit, it attacks (sucking the ChipWits’ fuel) instead of moving

The Actual Forth Code

From the MacForth source code on a 3.5 disk I was able to extract the relevant Forth code. Let’s see how close I came to the actual algorithm! Here’s the relevant code:

( Creep.move)                                     ( 110584 dws)
: ?zap.cw ( sq# ---flag)
 robot.square @ = not dup not ( cw is there, zap it)
if 6 flash.cw -200 update.fuel then ;
: Creep.move ( creep#/sq# ---)
 3 irnd 1 = if  ( 33% try to move)
   dup  toward.cw   ( creep#/sq#/next sq#)
dup dup dup square.object floor@ = swap ?zap.cw and
    swap robot.square @ squares.wide@ - = not and
    if  dup 4 roll creeps( + c!  ( sq#/nextsq#) ( safe to move)
       swap destroy          ( nextsq#)
       dup room.data( + creep@ swap c!  (  store in room)
    else drop swap drop then   ( sq#)
  else swap drop       ( sq#)
  then draw.random.creep ;

This is real source code from 1984 ChipWits! But yikes… what does all of this mean?!

Forth code is incredibly concise and, some would say… elegant? The entire ChipWits source code for Mac is approximately 3,000 lines of Forth code, compared to the current 35,000 lines of C# code we have in the game so far. But reading the Forth code is significantly more difficult, especially for someone (like myself) who never had the pleasure of writing Forth in the past.

Let’s break this down together, word by word. (Readers familiar with Forth, please comment if I got any of this wrong!)

( Creep.move)                                     ( 110584 dws)

The first thing I learned is that Electrocrabs were originally called “creeps” in the original source code. This is a very fitting name given how they move around and make chirpy noises. Very creepy, especially in swarms! Anything in parentheses in Forth is a comment, so this line can be ignored.

Stack-oriented Language

Forth is a stack-oriented language. Stacks are simple “LIFO” (last-in, first-out) data structures similar to a stack of dishes. You can put things on the top, and take them off the top, but it is difficult to remove things from the middle. Forth uses RPN (Reverse-Polish notation) for doing math. So, to add two numbers in Forth, you would do 3 4 + meaning “Put 3 on the stack. Put 4 on the stack. Add the top two numbers on the stack.”

To make things easier to understand, I’ll periodically show the state of the stack as we walk through the code.

?zap.cw

: ?zap.cw ( sq# ---flag)

This line defines a new “word” we can use in our Forth vocabulary, called ?zap.cw. Yes, words in Forth can start with ?. It is good form in Forth to follow your word definition with a comment. The comment in parentheses helpfully tells us what parameters are expected on the stack before you use this word. In this case, it expects you to place a square number and it leaves a “flag” on top of the stack when it is done.

Stack: <sq#>

 robot.square @ = not dup not ( cw is there, zap it)

Here, we put the address of the variable robot.square on top of the stack. This variable holds the square number containing the ChipWit. The symbol @ replaces the address with the value at that address. The symbol = compares to see if it is equal to the square number passed in. Then not inverts the value (true (non-zero) becomes false (0) and vice-versa). So far, we’ve effectively answered the question “is the ChipWit not at the square being zapped?”

Next, we dup, meaning to make a copy of the top of the stack, and not it again. So we will have two inverted boolean values at the top of the stack, the top of which answers the question “is the ChipWit at the the square being zapped?”.

Stack: <not-at-square?> <at-square?>

if 6 flash.cw -200 update.fuel then ;

The if in this statement consumes the boolean at the top of the stack and executes all the code until the then if the thing at the top of the stack is true, else it skips to the code after then. So, if the ChipWit is at the square, this executes, else it does not.

Assuming the ChipWit is at the desired square, we will put 6 on the stack, and then do flash.cw, which flashes the ChipWit by drawing an XOR mask on top of the ChipWit, in this case 6 times. It then puts -200 on the stack and calls update.fuel which subtracts 200 from the player’s fuel.

What’s left at the top of the stack is 1 if the ChipWit is not at the square in question, or 0 if so.

Stack: <not-at-square?>

Phew, not bad for 3 lines of code!

Creep.move

Now, let’s look at the Creep.move word definition:

: Creep.move ( creep#/sq# ---)

Here, we can see Creep.move expects two variables at the top of the stack, the creep id number and the square number:

Stack: <creep#> <sq#>

Roll the dice

 3 irnd 1 = if  ( 33% try to move)

Here, we put 3 on the stack and call irnd which is a word defined elsewhere in the program to pick a random number and mod it by what’s at the top of the stack. So this puts a number between 0 and 2, inclusive, on the stack. Then it puts 1 on the stack and compares to see if it equals 1. If so, it will do the following logic, else not.

Stack: <creep#> <sq#>

   dup  toward.cw   ( creep#/sq#/next sq#)

Now, we duplicate the square number at the top of the stack and call toward.cw, a word defined elsewhere in the program which takes a square number and replaces it with the neighboring square that is closest to the ChipWit.

Stack: <creep#> <sq#> <nextsq#>

dup dup dup square.object floor@ = swap ?zap.cw and

Now we load up the stack with 3 more copies of the next square number, followed by square.object which is a word that looks up the provided square number and returns the value of the object at that square. Next, we put the constant for the empty floor tile on the top of the stack.

Stack: <creep#> <sq#> <nextsq#> <nextsq#> <nextsq#> <object-at-nextsq#> floor@

Next, = compares the top two elements, answering the question “is the object at the square closest to the ChipWit a floor tile?” And we swap the top two elements of the stack:

Stack: <creep#> <sq#> <nextsq#> <nextsq#> <object-at-nextsq-is-a-floor?> <nextsq#>

Now, we call ?zap.cw which we defined above. Recall it takes a square number, zaps the ChipWit if it’s there, and replaces it with 1 if it is not there, or 0 if it is there.

Stack: <creep#> <sq#> <nextsq#> <nextsq#> <object-at-nextsq-is-a-floor?> <chipwit-not-at-nextsq>

The final and on this line checks if the top two elements on the stack are non-zero. In other words, is it true that the ChipWit is not at the next square and that the object is a floor tile? In other words, is the next square an empty tile we can move into?

Stack: <creep#> <sq#> <nextsq#> <nextsq#> <nextsq-empty?>

    swap robot.square @ squares.wide@ - = not and

Okay. Now, we swap the top two elements of the stack, put the ChipWit’s square number on the stack, put the number of squares wide (8), and subtract them. Since the board is stored as a 64-element contiguous array, this give us the square one row above the ChipWit.

Stack: <creep#> <sq#> <nextsq#> <nextsq-empty?> <nextsq#> <square#-above-robot>

Now we compare the top two elements and not the result (is the next square not above the ChipWit?) and then we and it with the result at the top of the stack, answering the question “Is the next square not above the ChipWit and is it empty?” I’m not entirely sure why we care whether the square is above the ChipWit, but it seems Electrocrabs don’t like to move to that square.

Stack: <creep#> <sq#> <nextsq#> <nextsq-not-above-robot-and-empty?>

    if  dup 4 roll creeps( + c!  ( sq#/nextsq#) ( safe to move)
       swap destroy          ( nextsq#)
       dup room.data( + creep@ swap c!  (  store in room)

Okay, now we reach a decision-point. If the square is safe to move to, we do some things, else we do some other things.

Decision point: Square is safe to move to

Stack: <creep#> <sq#> <nextsq#>

Let’s look at the code between the if and the else first. First, we dup and put 4 on the stack. Then we roll. In Forth, roll picks the nth element from the top of the stack and rolls it to the top. This is kind of like picking a dish from the middle of the stack. In this case, we pick the creep number.

Stack: <sq#> <nextsq#> <nextsq#> <creep#>

The creeps( array has at most 12 elements in it and stores the square number of each creep. We add the creep number to the array address and c! stores the 8-bit value of the next square number into the array at that location, effectively moving the creep. Finally, we swap bringing the old square number of the electrocrab to the top of the stack.

Stack: <nextsq#> <sq#>

Now call destroy, which updates the board (and redraws the graphic of the board), removing what was at the target square number.

Stack: <nextsq#>

Then, we dup the next square number, put the address of the room.data( array on the stack, and add the next square number, and place a creep@ at that index with swap and c! (store).

Stack: <nextsq#>

Decision point: Square is not safe to move to

Stack: <creep#> <sq#> <nextsq#>

If the square is not safe to move to, we take a different path:

    else drop swap drop then   ( sq#)

The sequence drop swap drop leaves us with:

Stack: <nextsq#>

If the Dice Roll Failed

Stack: <creep#> <sq#>

Back to if the dice roll failed…

  else swap drop       ( sq#)

The swap drop will leave the stack in this state:

Stack: <sq#>

Draw the Creep

We’ve reached the final statement:

  then draw.random.creep ;

Th draw.random.creep word draws the creep at the square number at the top of the stack (the new square if we rolled a 1, else the new square if we rolled a 2 or 3.

Reflections

It’s a really fun exercise to decipher the original Forth code for a hit game. We can learn quite a bit.

Though Forth code is concise, we can see how difficult it can be to analyze and how easy it is to leak memory or access unprotected areas of memory. Modern languages optimize for readability, protection, and saving human time. But there is something beautiful about the simplicity and efficiency of Forth.

My original reverse engineering of the Electrocrab came pretty close but differed in a few important ways:

• The electrocrab doesn’t seem to differentiate between “turning” and “pouncing”
• The chance the electrocrab moves is 33%, not 37.5%
• The electrocrab never moves to the square above the ChipWit (still not sure why!)

Discussion

What are your thoughts on this peek into the original source code of ChipWits? If you are a Forth expert, did I get this more or less right? Do you have any memories to share of coding in Forth? We’d love to hear your thoughts in the comments below!