Why is Random COINFLIP an OP?

When Mike and I developed ChipWits to the point where we could play it, we realized that we needed to add some randomness to IBOL. Let’s see why it was important to add the random COINFLIP operator, and get a preview of the dev gameplay while we’re at it!

Without a bit of randomness, ChipWits tend to get stuck in ruts — repeating the same moves over and over. Boring and literally and figuratively pointless.

Here’s a short program for the Greedville Mission, a mission in which there are only good THINGs to PICKUP. If the CW doesn’t feel a FLOOR, WALL, or DOOR it does a PICKUP. If it feels a FLOOR or DOOR it goes straight. If it feels a WALL it turns LEFT.

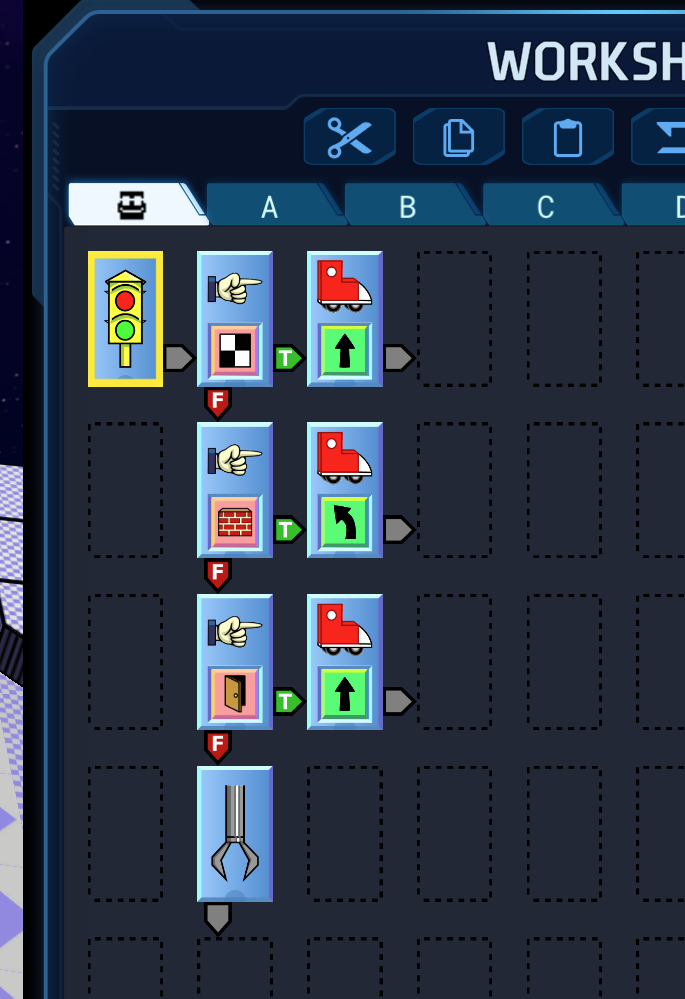
In this room the ChipWit gets stuck in a pattern. It follows the walls until it runs out of cycles. In different rooms this ChipWit gets stuck in other patterns of movement. Note: this video does not yet use our new graphics.

Play

A ChipWit that follows the same path over and over doesn’t score many points.

What could be more simply random than a coin flip? We added COINFLIP to IBOL. COINFLIP is a branching OP which branches TRUE or FALSE with 50/50 probability.

Below is the same IBOL program with two added chips, a COINFLIP which either does nothing or SKATEs LEFT. So sometimes when a CW feels a WALL it turns left twice.

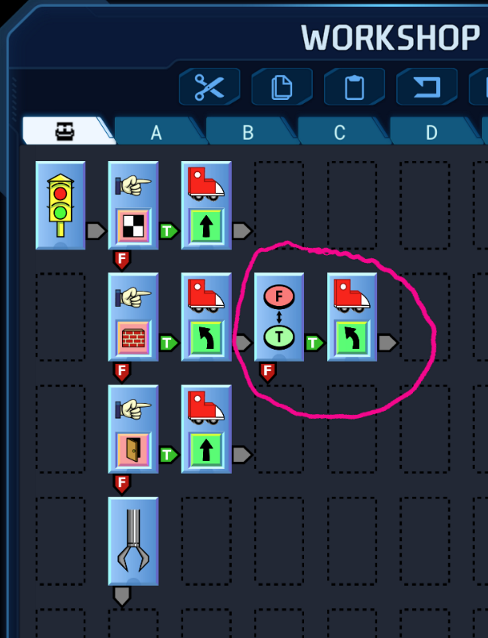
Adding a random turn breaks the ChipWit out of its rut and lets it hunt for points.

Play

When you add a COINFLIP to a ChipWit it becomes unpredictable. It may seem counterintuitive that an unpredictable ChipWit can perform better than a predictable one.

When your ChipWit keeps getting stuck, make it flip a coin to break the pattern.

IBOL TIP: If you want a random result that is less than 50%, chain COINFLIPs together.

In the program below 3 COINFLIPs are chained. What is the probability that the SKATE RIGHT chip executes?
Hint: Each COINFLIP has a 50% chance of branching TRUE. Multiply the probability of each chip in the chain to get the probability of hitting the SKATE RIGHT chip.

Discussion

What are your thoughts on the COINFLIP IBOL operator? Have you ever built an interesting robot or other automaton that makes interesting use of random behavior? Post your comments below!